* 투영행렬 ( Perspective Matrix ) 결과

g(z) = A + B / z
g(n) = 0
g(f) = 1
을 이용해서 A,B 를 구할 수 있었다.
하지만, 항상 또 다른 문제가 발생하기 마련이다.
우리가 near, far 에 따라서
z 값을 [ 0~1 ] 사이의 값으로 맞추기 위해 만든 g(z) 함수 와 z 값 사이에 문제가 발생한다.
*Z-Fighting ( 정밀도 문제 )
z ( 깊이 ) 의 낮은 정밀도로 인해서 물체가 겹쳐보이는 현상이 발생.
무슨말인가 ??
위에서 우리가 구한 g(z) 함수는 '비선형' 함수 이다.
즉,
일차방정식처럼 일정한 방향으로 늘어나지 않고
이차함수처럼 곡선이다.



그래프를 참고하면 'near' 값이 엄청난 영향을 끼친다 는 사실을 알 수 있다.
near 의 값이 0 에 가까울수록 앞 부분에서는 간격은 좁아져서 세밀하게 표현할 수 있지만
뒷부분에 갈수록 간격은 넓어진다.
즉,
마지막 그림 왼쪽 좌표 d 에서 마지막 z = 1 이전의 부분에는
엄청나게 많은 z 값들이 해당 범위 안에서 표현되어져야 한다.
선형 처럼 1 : 1 방식으로 매칭되지 않는다는 말이다.
이 때,
z 값 인근에 위치한 z 값들과 값이 같아지는 현상이 발생.
깊이가 같아져버린다!!
이 현상을
'Z-Fighting' 이라고 불린다.
서로 같은 깊이로 계속 싸우고 있는 것처럼 렌더링되어진다.
해당 현상을 테스트 하기 위해 간단한 코드를 구현해보자.
( g(z) 식을 옮겨놓은 코드. )
( cout.precision 은 따로 설정하지 않을 것.
최대 24 로 늘리고 한다고 해도 결국 같은 결론 도출. )
float n = 1.f, f = 100.f;
int z = n;
for (; z <= (int)f; ++z)
{
float A = f / (f - n);
float B = (-1) * (f * n) / (f - n);
float result = A + (B / z);
cout << z << " : " << result << endl;
}

=> 코드를 실행하면,
그래프처럼 굉장히 가파르게 범위가 올라가는 것을 볼 수 있다.
*해결방법
=> 자, 이제 어떻게 이 문제를 풀어야 할까 ??
참고한 DX 책에서는,
n 과 f 의 거리를 좁히는 것을 추천하고 있는데
위에 있는 코드에서 n = 10.f 로 바꾸고 실행해보자.

=> 이전에 n = 1.f 일 때보다는 덜 가파르게 증가하는 것을 볼 수 있다.
하지만 이것이 근본적인 해결책일까 ??
언제까지고 near 값을 무한정 늘릴 순 없다.
또한, z 값이 큰 오브젝트들은 결국 깊이가 겹칠 것이다.
뛰어나신 선대분들이 해결책을 내놓으셨다.
바로 'depth 범위를 뒤집는 방법' 이다.
'Reversed Z' 라고 부른다.

=> 그림에서 나오는 것처럼
왼쪽 좌표 d 의 범위를 [ 1~0 ] 으로 바꿔주기만 했는데 효과가 엄청난 걸 볼 수 있다.
눈으로 직접 봐보자.
코드로 비교하기 앞서
우선,
비교를 위해서 이전 코드 n = 10.f , f = 10000.f 로 실행해보자.


=> 역시 예상대로 z 값이 높아질수록 중복되는 횟수가 많아진다.
이제 n <---> f 를 반대로 매칭해보자.
g(n) = 1 / g(f) = 0
float n = 10000.f;
float f = 1.f;
int z = n;
for (; z >= (int)f; --z)
{
float A = f / (f - n);
float B = (-1) * (f * n) / (f - n);
float result = A + (B / z);
cout << z << " : " << result << endl;
}
*실행결과

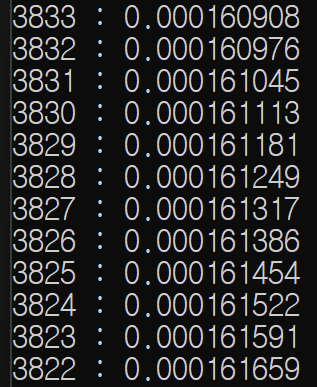

near 일 때 = 1, far 일 때 = 0 이 나오도록 설정만 했을 뿐인데,
1 ~ 10000 까지의 z 값이 모두 독립적인 것을 볼 수 있다.
해당 Reversed Z 방식은 무한대 far plane 에서도 잘 구별할 수 있다고 한다.
*결론
ClipSpace 에 원근법을 적용해 좌표계 변환을 하기 위해 투영 행렬을 만들었다.
그렇지만 투영 행렬로 좌표의 깊이 (z) 값을 [ 0~1 ] 로 만들 때 문제점이 한가지 있다.
바로 'Z-Fighting' 이다.
원인은 투영행렬의 m33, m43 에 해당하는
n, f 에 따라 [ 0~1 ] 에 사상되어지게 하는 식에서 문제가 발생한다.
g(x) = A + B / z
( z 값 나누기까지 된 상태. )
A = f / ( f - n )
B = - nf / ( f - n )
해당 함수는 '비선형' 함수이다.
결과값들을 그래프로 그려보면 곡선형태로 되어있는 걸 볼 수 있는데,
문제는 곡선의 기울기가 너무 완만해서
[ 0~1 ] 사이의 특정부분에만 값들이 집중되어지는 현상이 발생.
이 때, 깊이 (z) 값 차이가 미세할 때 같은 결과값이 같아버리게 된다.
해당 문제의 해결방법은
'Reversed Z'
Z 값을 [ 0~1 ] 사이로 만드는 것을 반대로
Z 값을 [ 1~0 ] 사이로 맵핑시킨다.
즉,
g(n) = 1, g(f) = 0 이 성립되도록 조건을 만들게되면
Z-Fighting 문제가 해결된다.
참고 자료
'DirectX > 개념' 카테고리의 다른 글
| [DX] ##7. GJK ( GILBERT-JOHNSON-KEERTHI ) Algorithm (0) | 2022.08.15 |
|---|---|
| [DX] ##6. AABB, OBB 충돌 SAT 분리축 이론( Separating Axis Theorem ) (0) | 2022.08.05 |
| [DX] ##5. 직교투영, Screen Space ( Window Space ) (0) | 2022.08.02 |
| [DX] ##2. Local, World, View Space (0) | 2022.07.29 |
| [DX] ##1. 좌표계 변환 (0) | 2022.07.28 |