*3D 그래픽스를 처음 접했을 때의 궁금증
*행렬을 사용하는 목적
=> 3차원을 표현하기에 적합하다.
=> 선형변환을 적용할 수 있다.
*선형변환이란 ??
간단하게 설명하자면,
어떤 값 : A 라고 할때,
A + ( 어떤 연산 ) = B
즉,
A 에 어떤 연산 을 적용했을 때, 모든 계산된 값은 B 이어야 한다.
이 때, 어떤 연산을 '선형' 이라고 한다.
또, 이 과정을 '선형변환' 이라고 한다.
벡터는 크기를 늘이고 줄일 수 있다. 또한, 방향도 가지고 있다.
어떤 벡터를 어떤 점에 적용했을 때, 이동한 점을 알 수 있고
반대로 적용한 벡터를 알고 있다면, 다시 원래대로 되돌아올 수 있다.
즉, 벡터는 명백히 '선형' 이다.
따라서, 벡터는 선형이고 어떤 벡터들을 어떤 점이나 다른 벡터에 적용하는 것이
선형변환이라 볼 수 있겠다.
3차원에서는 이 벡터를 3개까지 늘려서 3차원 벡터에
선형변환을 적용해 3차원 벡터를 나오게 하는 것이다.
벡터를 3개까지 늘린다고 했는데 주의해야할 것은
'각각의 벡터가 한 차원을 가리키는 기저벡터' 라는 것이다.
이것이 의미하는 것은
3개의 축으로 우리가 원하는 좌표계를 설정할 수 있고
해당 좌표계를 어떤 벡터나 다른 행렬에 적용할 수 있다는 이야기이다.
즉, 기준을 바꿔간다고 생각하면 된다.
예를 들어,
간단하게 2D 로 생각해보자.
공간 : 어떤 좌표계가 적용된 곳.
어떤 공간의 기준은 기존의 공간에서,
x 축으로 -5, y 축으로 2 만큼 이동한 것이라고 가정할 때,
우리가 알고 있는 일반적인 2D 평면에서의 ( 1, 1 ) 은
해당 공간으로 이동하게 되면 (-4, 3) 인 좌표가 된다.
그 공간에서의 ( 1,1 ) 은 ( -4,3 ) 이라는 소리이다.
이번엔 반대로,
x 축으로 5, y 축으로 -2 만큼 이동한 기준을 더하게 되면
원래 좌표인 ( 1,1 )이 된다.
( -5, 2 ) 의 역행렬은 ( 5, -2 ) 이라는 소리이다.
이제 이 과정을 3D 로 확장시키고 적용하면
그것이 3D 에서의 좌표계 변환이 된다.
*왜 4차원 행렬을 계산해야하는 걸까 ??
3차원이라면 3개의 축을 나타내는 3x3 행렬로 계산하면 되지 않을까 ??
어떤 3차원 벡터와 3차원 행렬 끼리 계산할 때,
축을 바꾸고 크기를 늘리고 줄일 수 있지만,
단지, 3차원 벡터를 이동을 해야하는 상황이라면 ??
( x,y,z ) * (3x3 행렬) => ( x+a, y+b, z+c ) 가 되어야하는데
일반적인 행렬 계산법으로는 저런 결과값이 나올 수가 없다.
하지만, 한 차원을 늘리게 되면 가능 하다.
( 열 벡터 기준 )
| 1,0,0,a | * | x | = | x + a |
| 0,1,0,b | | y | = | y + b |
| 0,0,1,c | | z | = | z + c |
| 0,0,0,1 | | 1 | = | 1 |
만약,
방향을 나타내는 벡터라면 ( x,y,z,0 ) 으로 표현될 수 있다.
마지막 w = 0 이라면 a,b,c, 는 적용되지 않는다.
반대로 벡터를 위치로 나타내 이동계산을 하고 싶다면 w = 1 로 두면 된다.
즉, 이동이 적용되지 않는다는 소리.
*결론
* 선형변환
어떤 값들에 어떤 연산이 적용될 때, 어떤 값들에 대한 어떤 연산의 값이 항상 같다면,
선형변환이라고 말할 수 있다.
* 좌표계 변환
3차원의 축, 점 들을 표현하기 위해 벡터를 사용,
벡터를 표현하기 위해 행렬을 사용하고
그와 동시에 행렬이 선형변환 역할까지 수행.
좌표계를 표현한 행렬들을 이용해
어느 하나의 점이 화면에 그려지기까지의 일련의 과정.
*하나의 점이 화면에 보여지기까지의 과정
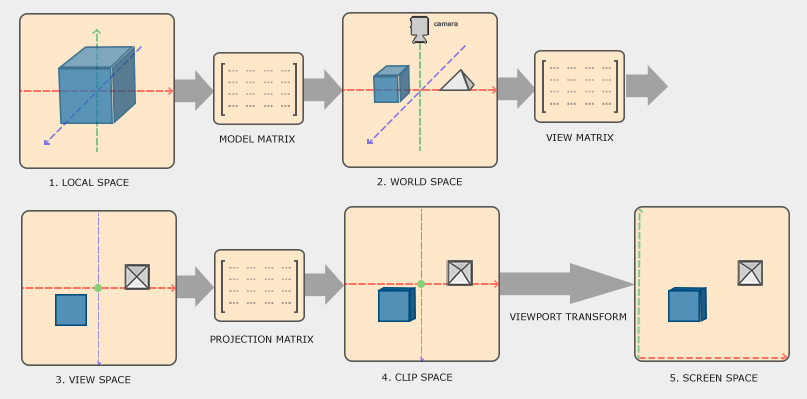
LocalSpace -> WorldSpace -> ViewSpace -> ClipSpace, NDC -> ScreenSpace
해당 과정을 하나하나 살펴보자.
'DirectX > 개념' 카테고리의 다른 글
| [DX] ##7. GJK ( GILBERT-JOHNSON-KEERTHI ) Algorithm (0) | 2022.08.15 |
|---|---|
| [DX] ##6. AABB, OBB 충돌 SAT 분리축 이론( Separating Axis Theorem ) (0) | 2022.08.05 |
| [DX] ##5. 직교투영, Screen Space ( Window Space ) (0) | 2022.08.02 |
| [DX] ##4. Z-Fighting (0) | 2022.07.31 |
| [DX] ##2. Local, World, View Space (0) | 2022.07.29 |