* 애니메이션 ( ANIMATION )
게임에서의 애니메이션은 어떻게 표현될까 ??
그전에 사람이 정점으로 3D 에서 어떻게 표현되는지 알아보자.
게임 엔진에서 애니메이션을 실행하거나 Mesh 를 보면 많은 점들로 이루어진 사람 모양의 형태를 볼 수 있다.
흔히 이런 골격 표현을 "Skeleton" 이라 부르고 뼈에 해당하는 부위를 "Bone" 이라 부른다.
* Skeleton
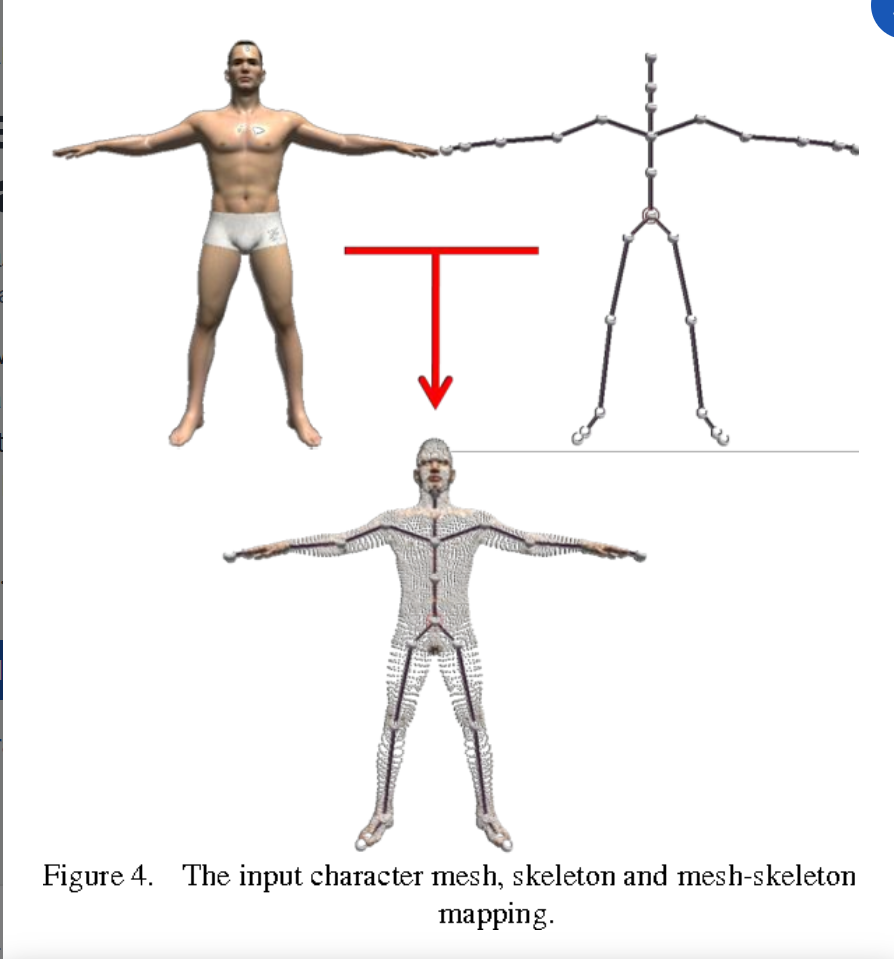
위 그림처럼 흔히 대자로 뻗은 사람 모형 Skeleton 을 형상할 때, "T-Poze 혹은 Bind Poze" 라고 부른다.
이 모형을 기준으로 우리는 골격을 이루는 뼈마다 해당 부분을 정점이라 생각하고
이 점들을 움직임으로써 인간 형태의 애니메이션을 적용할 수 있다.
이것은 컴퓨터에 정점을 표현해 어떤 물체를 그려내야하는 우리 입장에서는 굉장히 좋은 선택지이다.
Skeleton 을 이루는 Bone 들을 정점이라고 생각하자.
Skeleton 에는 맨 처음 기준이 되어지는 곳이 존재하는데 이곳을 'Root' 라고 부른다.
( 보통 배꼽, 발 중앙.. 등에 위치한다. )
Bone 정점들은 Root 좌표 기준으로 위치시키면 된다.
이 상태에서 어떻게 애니메이션을 적용해야할까 ??
모든 정점들을 하나하나 움직여야할까 ??
상상해보자.
우리의 기준으로 만약 우리가 팔을 들어올린다면 팔만 움직이는가 ??
손이 머리 위로 이동하고 팔꿈치와 어깨 또한 따라 올라간다. 이것은 매우 자연스럽다.
이 동작을 우리가 애니메이션으로 표현하기 위해선 정점들이 서로 관계되어야할 것이다.
우리는 점과 점의 관계를 형성하기 위해서 정점을 트리 형식의 계층 구조로 만들어야 한다.
상위 정점을 부모, 하위 정점을 자식이라고 칭할 때, 자식은 부모를 기준으로 위치한 정점 데이터를 가진다.
이 과정은 루트에서부터 연결될 수 있는 마지막 정점까지 이어진다.
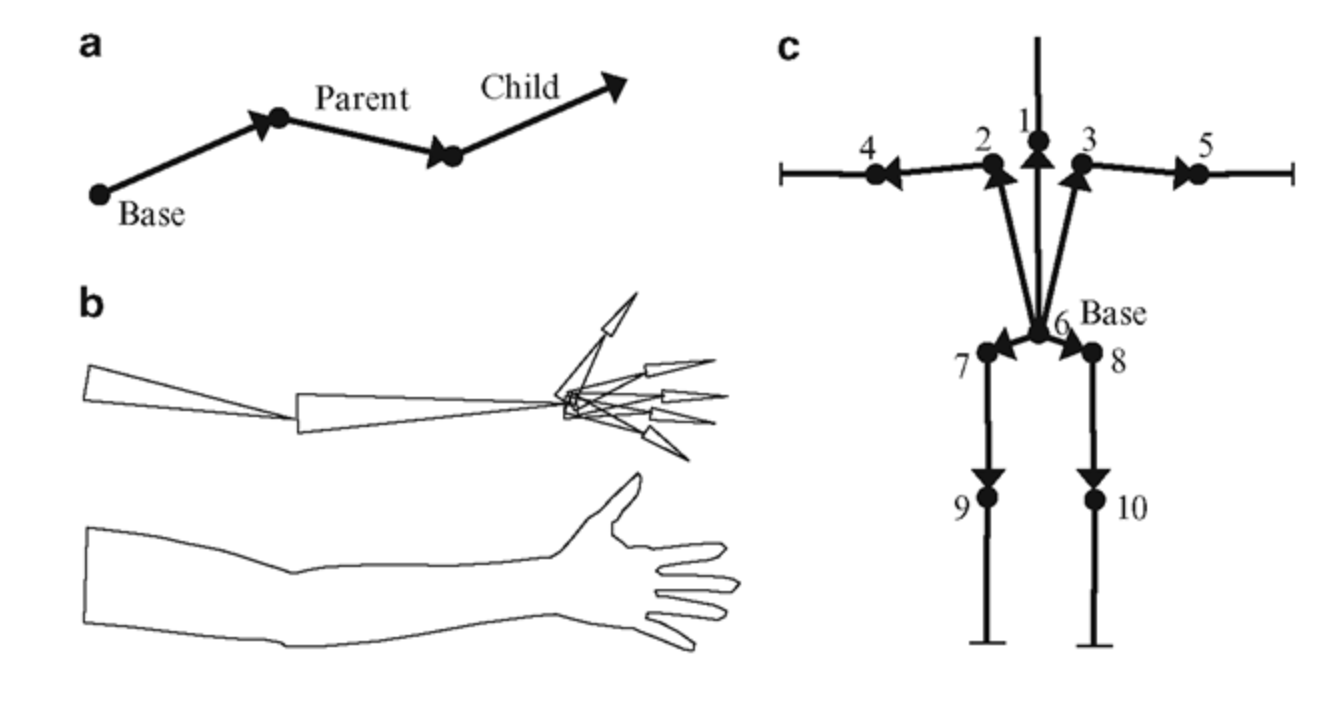
위 그림에서처럼 정점들이 이어지면서 사람 골격을 표현한 것을 볼 수 있다.
이 각각의 Bone 을 표현하는 점들을 'Joint' 라고도 부른다.
또, 추후 다루겠지만 자연스러운 애니메이션을 위해서
인접한 정점들의 영향을 얼마만큼 받을 것인지 '가중치' 에 대한 정보들과
해당 점들이 얼만큼 움직여야하는지에 대한 정보 또한 필요할 것이다.
물론, 우리는 프로그래머이기 때문에 애니메이션 동작을 정의하기 위해 정점을 조절하는 일은 거의 없을 것이다.
우리가 해야할 일은 이 과정을 이해하고 해당 데이터를 정상적으로 게임에 적용하는 것이다.
첫번째로 우리는 Joint Point 기준으로 표현되는 정점을 World Space 로 표현되는 과정을 이해해야한다.
* 오프셋 변환 ( Offset Transformation )

우리가 알고 있는 정보는 각 Bone 들이 계층 구조를 이루고 있고
부모를 기준으로 Bone 들이 어디에 위치하는지 알고 있으며 우리가 표현할 정점들이 어느 Bone 들에 속해있고
그 Joint 를 기준으로 정점이 어디에 위치해있는지에 대한 정보들을 가지고 있다.
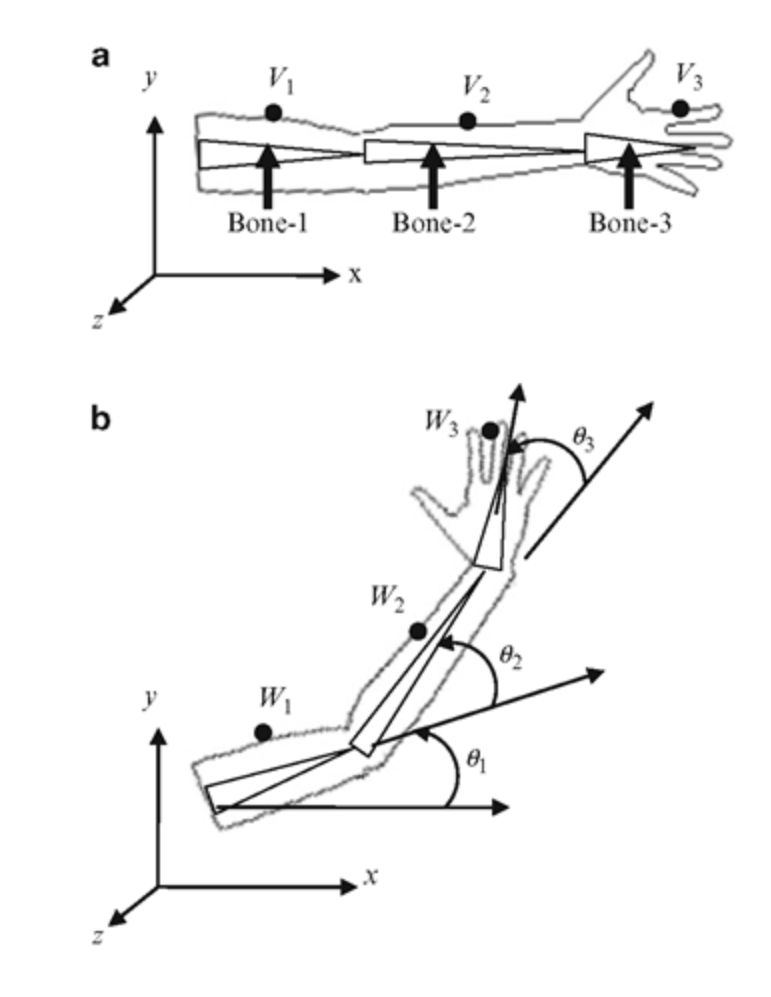
위 그림 b 부분에는 팔을 들어올리는 예시가 나와있다.
순서대로 Bone-1,2,3 을 기준으로 한 정점이 W1,2,3 이라고 할 때,
Bone-1 은 'Root' 를 기준으로 25 도 (대략) 돌린 축이다.
Bone-2 는 Bone-1 을 기준으로 25도 돌린 축이며 해당 축을 기준으로 W2 가 위치한다.
마찬가지로 Bone-3 도 Bone-2 를 기준으로 25도 돌린 축이며 이 축을 기준으로 W3 이 위치한다.
최종적으로 Bone-3 에 속해있는 W3 정점은 총 75도가 돌려진 정점이 된다.
Bone-3 기준에서 정점을 본다면 단지 25도만 돌려진 정점이 된다.
따라서, 우리는 해당 정점이 속한 Joint 까지의 선형 변환이 필요하다.
부모를 기준으로 위치한 Joint 정점의 행렬이 곧 선형 변환을 위한 좌표계가 된다.
Bone-1,2,3 위치 행렬을 계속 곱해 선형 변환함으로써 Root 좌표계 기준으로 표현된 정점을 구할 수 있다.
즉,
Root 에서부터 정점이 속해있는 Bone 행렬까지 곱하면 된다.
이 과정을 '오프셋 변환 ( Offset Transform )' 이라고 한다.
여기서 끝이 아니라, 추가적인 과정이 필요하다.
* 뿌리 변환 ( To Root Transformation )


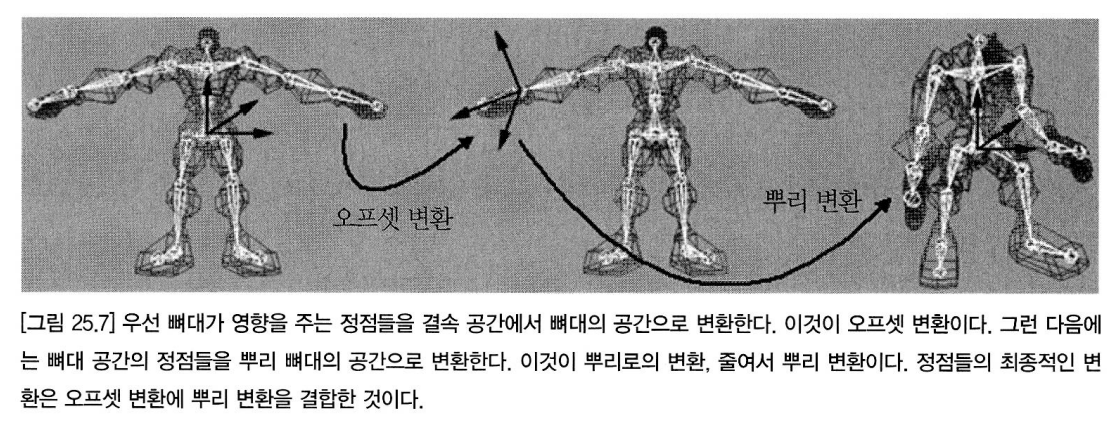
첫번째 그림은 Bone 의 계층 구조로 Bone 좌표계들을 시각적으로 표현한다.
두번째 그림은 부모 변환 행렬을 이용해 세계 공간에 도달하는 것을 표현한다.
여기서
Root 공간까지의 변환 행렬을 'To-Root 행렬' 이라 말한다.
또, 위 부모 계층까지의 행렬을 'To-Parent 행렬' 이라 부른다.
To-Root, To-Parent 둘 다 제공하는지 To-Parent 만 제공하는지 사용하는 애니메이션 툴에 따라서 다른다.
즉,
환경에 따라 다르기 때문에 상황에 맞게 계산할 필요가 있다.
중요한 것은 Root 좌표계로 표현된 정점을 다시 To-Root 까지의 선형 변환을 적용해야한다는 것이다.
우리가 실행할 애니메이션 자세에 해당하는 오프셋 변환과 Root 변환을 거치고 나면
현재 정점은 애니메이션에 알맞은 위치에 배치된다.
이 때, 두 번째 그림의 A0 까지의 뿌리 변환은 Root 의 Local Space 란 점이다.
이 후 World 행렬을 곱해 선형 변환해주어야 비로소 정점은 World 공간에 존재하게 된다.
여기서 의아한 점이 생긴다.
왜 부모 변환 행렬을 이용해 세계 공간에 도달해야할까 ??
이미 오프셋 변환의 결과로써,
Bone 좌표계로의 선형 변환을 통해서 Joint 에 기준한 정점은 이미 Root 좌표계에서 표현될 수 있다.
여기에 World 행렬만 곱해주기만 하면 World 좌표계로 표현될 수 있다.
* 왜 뿌리 변환이 필요한가 ??
잘 이해가 안되었던 부분이다.
DX 책을 참고하면 해당 Bone 까지 오프셋 변환 후에는 반드시 ToRoot 뿌리 변환이 필요하다고 언급된다.
현재 우리의 상황을 살펴봐야한다.
우리는 어떤 골격 ( Skeleton ) 을 애니메이션하려는 목적을 가진다.
애니메이션을 위해서 Skeleton 의 어떤 한 정점이 애니메이션 동작에 해당하는 정점의 위치로 이동한다.
여기서 시작인 골격은 무엇인가 ??
바로 위에서 본 'T-Pose' 이다.

처음 정점은 T-Pose 모양의 위치에 저장되어져있다.
이는 우리가 T-Pose 를 정의하는 이유가 정점의 초기 값 설정을 위함이라는 것을 파악할 수 있다.
어느 애니메이션 한 장면을 연출하기 위해 정점을 해당 위치까지 오프셋 변환을 수행한다.
이 후, T-Pose 모양을 원래대로 되돌리기 위한 To-Root 행렬을 곱하게 된다.
이 때, To-Root 행렬은 T-Pose 에서의 정점이 해당하는 Bone 행렬의 역행렬이 되겠다.
한마디로,
T-pose 의 위치한 정점 좌표에서 애니메이션 자세에 해당하는 정점 좌표로 바꾼다는 것이다.
그림에서의 a 그림을 b 그림으로 바꾼다는 것과도 같다.
위에서 본 그림을 이제 수식과 함께 보자.
B1, B2, B3 부분이 a 에 해당하는 수식이고 B'1, B'2, B'3 부분이 b 에 해당하는 수식이다.
초기 정점의 위치는 B1, B2, B3 이므로 우리가 W1, 2, 3 을 구하기 위해선
b 에 해당하는 수식에서 B1, B2, B3 의 역행렬을 곱하면 b 에 대한 정점의 위치를 얻을 수 있다.
Root 기점으로 선형 변환해온 좌표에 역행렬을 곱하는 것이기 때문에 이전으로 되돌아갈 수 있다.
( 적용된 선형 변환의 역행렬은 적용된 선형 변환을 다시 되돌리는 역할이다. )
* 최종 변환 ( Final Transform )
우리는 오프셋 변환 + 뿌리 변환 을 통해서 현재 애니메이션에서 해당 정점이 위치한 곳을 계산한다.
이 과정을 골격을 이루는 모든 정점마다 실행한다.
모두 선형 변환이므로 하나의 행렬로 표현하면 'F(i) = offsetMatrix(i) * ToRootMatrix(i)' 가 되겠다.
위 행렬을 '최종 변환 행렬 ( Final Transform Matrix )' 이라고 부른다.
주의할 점은 이는 아직 World Space 가 아니란 점이다.
최종 변환 행렬을 곱한 후, World 행렬을 곱했을 때, 비로소 정점은 World Space 에 있게 된다.
실제 프로그래밍에서 우리의 최종 목적은
주어진 애니메이션 데이터를 이용해 최종 변환 행렬을 구하는 것이다.
이 때, 우리는 2가지 방식 중 하나를 선택해야한다. 상향식, 하향식이 그것이다.
상향식은 Bone 기준으로 표현된 정점에서부터 Root 까지 뿌리 변환 행렬을 구하고
다시 Root 에서 해당 Bone 까지의 오프셋 변환을 계산한다.
여기서 오프셋 변환에서 계산 방향이 Root 에서 Bone 으로 향하는 방향이므로 무조건 Root 까지 도달해야하는 문제가 생긴다.
그로 인해, 처음 계산이 시작되는 Root 행렬을 알 수 없어서 최종적으로 Root 에 도달했을 때 한꺼번에 계산되어진다.
반면, 하향식은 Root 에서부터 시작해 해당 Bone 까지 찾아가면서 계산하는 과정이다.
이 때, 오프셋 변환 계산 방향이 일치하여 오프셋 변환 행렬을 구할 수 있고
뿌리 변환에서도 이미 부모를 거쳤기 때문에 반대의 계산을 수행함으로써 해당 Bone 까지의 행렬을 즉시 계산할 수 있다.
이러한 계산 효율성 때문에 '하향식' 을 채택한다.
한 가지 더 흥미로운 사실은 계산 효율성을 위한 또 다른 방법으로
Bone 마다 Index 를 부여하고 해당 Bone Index 까지의 오프셋 행렬과
ToRoot 행렬을 계속 계산하지 않고 저장하여 재활용한다.
저장한 행렬을 애니메이션 Clip 마다 설정된 좌표에 곱해주면서 World Space 에서의 정점으로 표현한다.
이는 '다이나믹 프로그래밍 ( Dynamic Programming ) 개념' 을 활용했다고 볼 수 있다.
* 스키닝 ( Skinning )
이제까지 Skeleton ( 골격 ) 에 해당하는 개념을 살펴보았다면, 이제 Bone 에 소속된 정점들을 다뤄보자.
특정 Bone 을 기준으로 여러 개의 정점들을 사람의 피부처럼 표현하는 방법을
'스키닝 ( Skinning )' 이라고 한다.
여기서 특정 Bone 을 '결속 공간 ( Bind Space )' 라고도 부른다.
Bone 좌표와 마찬가지로 붙어있는 모든 정점들도 애니메이션마다 지정된 위치들로 이동되어진다.
보통 'Key Frame Animation ( 키 프레임 애니메이션 )' 방법을 사용한다.
이는 Frame 마다 정점들의 위치를 정의해놓음으로써
계속해서 Update 되면서 정점들이 이동하며 애니메이션을 표현한다.
만약,
Frame 마다 정점들이 바로바로 바뀌도록 입력되어지면 애니메이션이 매끄럽지 못하게 재생되기 때문에
해당 Frame 에서 다음 Frame 으로 이동될 때, 보간법을 이용한다.
( 추후에 다시 다룬다. )
추가적으로 이렇게 Animation 이 정의되어있는 것을 통틀어 'Animation Clip' 이라고 부른다.
예를 들면, 걷기, 뛰기, 정권찌르기 같은 애니메이션 클립이 있을 수 있다.
* 정점 혼합 ( Transformation Blending )
위에서 설명할 때에는 정점 하나가 특정 Bone 에만 속해있다고 했지만 실제론 그렇지 않다.
사람 피부를 표현하는 정점은 여러 Bone Joint Point 에 영향을 받을 수 있다.
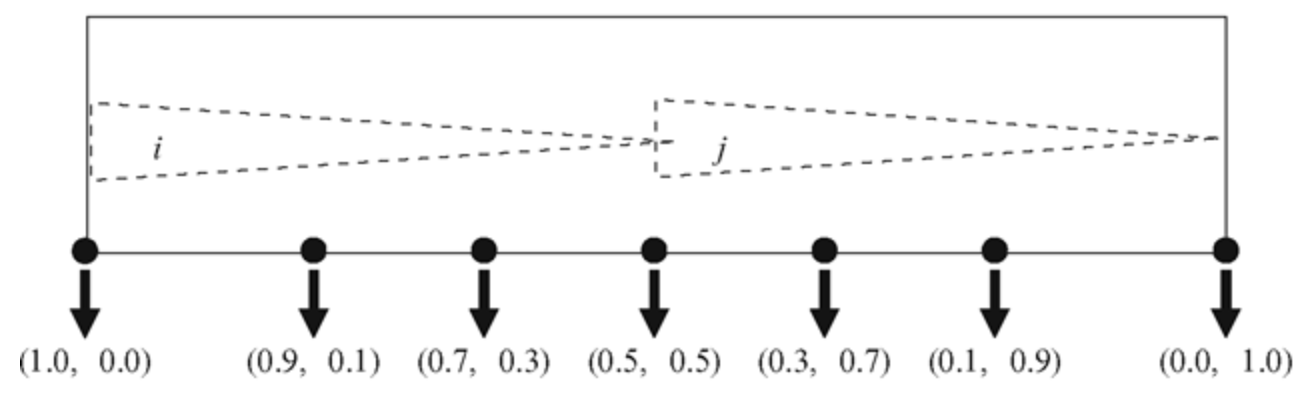
만약 위 그림처럼 2개의 Bone 만 존재한다고 가정할 때,
까만색 정점들은 Skin 을 나타내는 정점이며 이 정점은 Bone(i), Bone(j) 2개의 Bone 에 영향을 받는다.
이처럼 영향을 받는 Bone 들마다 얼마큼의 가중치를 둘 것인지를 설정하고
이 가중치만큼 정점의 최종 선형 변환 ( Final Transform ) 에 적용하는데 이것을 '혼합 ( Blending )' 이라고 한다.
이 때 모든 가중치의 합은 1 이어야하며 4개의 가중치 정도면 어느 정도 매끄럽게 표현 가능하다고 한다.
여기서 가중치 W 의 총합이 1 이어야하는 이유는 '비율' 이기 때문이다.
1 이 아니라면, 우리가 원하는 값에서 더 크거나 더 작은 값이 될 것이다.
따라서, 1 : 1 비율로 섞는다는 것은 반반 0.5, 0.5 의 양을 계산하는 것과 같다.
하지만 이런 Blending 계산에는 몇 가지 문제가 발생한다.
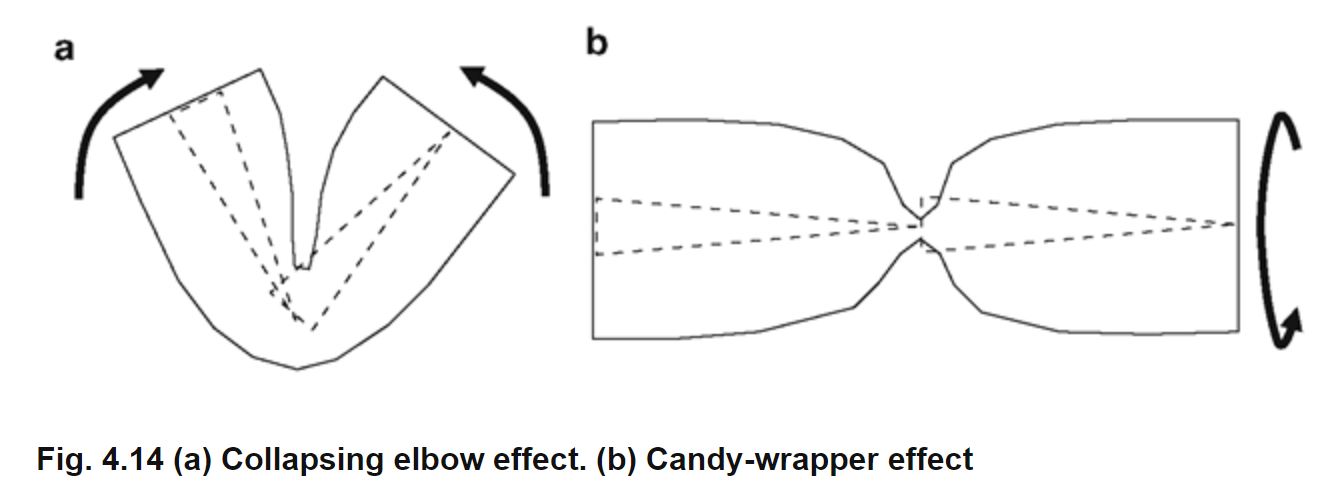
첫번째 그림은 'Collapsing Elbow Effect' 현상을 표현한다.
두 인접한 Bone 축들이 가까워질 때, 팔을 구부리는 동작처럼
두 Bone 축의 회전 차가 커질 경우 발생한다.
두번째 그림은 'Candy-Wrapper Effect' 현상을 나타낸다.
이는 첫번째 상황과 다르게 같은 축을 기준으로 회전 차가 커질 경우 발생한다.
두 가지 현상의 근본적인 문제는 회전을 선형으로 Blending 하기 때문이다.
즉,
Joint Point 가 회전할 때 이동되는 Skin 정점 사이를 회전한 경로를 따라서 선을 이어주어야하는데
선형으로 이어주게되면서 일정 부분 면적이 날아가고 이러한 이유로 비어보이게 된다.

LBS ( Linear Blending Skinning ) 는 선형 Blending 으로 정점을 잇는 방법이며
이를 해결하기 위해서 우리는 구형 Blending 을 위한 'SBS ( Spherical Blending Skinning )' 방법을 사용해야한다.
또, 이를 위해 사원수 ( Quaternion ) 을 사용한다.
( 위 링크 참고 시 자세한 내용 확인 가능, 사원수 'Quaternion' 는 조만간 다룰 것. )
* Key Frame Animation
앞서 Skinning 단락에서 살펴본 것처럼 Key Frame Animation 은 Frame 마다 Joint Point 의 위치를 설정한다.
이 정보를 토대로 Frame 마다 Skin 을 표현하는 정점들이 움직이며 애니메이션을 연출하는 방법이다.

위 그림은 간단하게 Key Frame Animation 을 설명하고 있다.
총 4 Frame 안에 4 가지 동작들이 정의되어있고 이 동작들이 연속되어지면서 애니메이션을 연출한다.
이 때, Frame 마다 어느 정도 시간이 존재하기 때문에
자연스러운 애니메이션을 위해선 이 틈을 보간하는 방법을 필요로 한다.

a 그림은 보간을 하지 않기 때문에 장면들이 뚝뚝 끊겨보이는 현상이 발생할 것이다.
b 그림은 선형 보간을 통해서 Frame 사이를 보간한다.
c 그림은
우리가 Blending 에서도 살펴본 것처럼 회전을 선형으로 보간하기 때문에
회전하는 동작 애니메이션이 발생할 때, Mesh 에 일정 부분이 비어지고 부자연스럽게 보일 것이다.
이를 해결하기 위해서 Spline 보간법을 이용한다.
* 결론
이제까지 애니메이션은 어떻게 구현되고 동작하는지에 대해 원리를 살펴보았다.
대략적으로 정리해보자.
실제 사람처럼 뼈마디에 해당하는 Bone 들을 정하고 사람 골격에 해당하는 Skeleton 으로 표현한다.
컴퓨터는 정점을 화면에 표현하기 때문에
여기서 Bone 들을 정점으로 표현하고 사람 피부를 표현하기 위해 정점을 위치시킨다.
팔을 들어올리면 어깨가 들리듯이 정점들의 관계성을 위해서 Joint 정점들을 계층 구조로 설정되고
이로 인해 Mesh 정점들은 Joint 정점을 기준으로 위치가 정의된다.
어떤 동작을 정의하기 위해서 정점들을 표현해야하는데 2가지 과정을 거친다.
동작에 위치하는 정점으로 가기 위해 연관된 Joint 까지의 선형 변환 과정과
기존 초기에 설정된 동작 위치를 되돌리는 역행렬 과정이다.
정점은 하나의 Bone 에만 연관되어지지 않고 여러 Bone 에 연관되어질 수 있다.
연관된 Bone 들의 비율들을 '가중치' 로 설정할 수 있고 총 합은 1이 되어야 한다.
여러 연관된 Bone 들 사이의 회전 수치를 선형으로 Blending 하게 되면
Mesh 가 잘려지거나 이상하게 보이는 문제점이 있기 때문에 구형으로 Blending 해야한다.
Bone 들의 위치를 정의해서 Frame 마다 애니메이션을 실행시키는 방법을 Key Frame Animation 이라고 한다.
Frame 사이에 약간의 간격이 존재하므로 자연스러운 애니메이션을 위해 보간이 필요하다.
Blending 에서도 마찬가지로 정점 사이를 보간 시, 선형 보간보다 구형 보간이 자연스럽다.
( 다음은 Quaternion 과 Spline 에 대해서 다뤄볼 예정이다. )
참고 자료
- 프랭크 D.루나. ( DirectX11 을 활용한 3D 게임 프로그래밍 입문 ), 류광(역)
'DirectX > 개념' 카테고리의 다른 글
| [DX]##3. 원근 투영 ( Perspective Projection ) (0) | 2022.12.16 |
|---|---|
| [DX] ##8. FRUSTUM CULLING ( 절두체 선별 ) (0) | 2022.08.25 |
| [DX] ##7. GJK ( GILBERT-JOHNSON-KEERTHI ) Algorithm (0) | 2022.08.15 |
| [DX] ##6. AABB, OBB 충돌 SAT 분리축 이론( Separating Axis Theorem ) (0) | 2022.08.05 |
| [DX] ##5. 직교투영, Screen Space ( Window Space ) (0) | 2022.08.02 |