* GJK Alogrithm
SAT ( 분리축 이론 ) 과 더불어 다각형 충돌 처리에 쓰이는 알고리즘이다.
SAT 보다 상대적으로 비용이 저렴하고 빠르다.
우선 대략적인 개념을 알아보고 어떤 식으로 구현할지 알아보자.
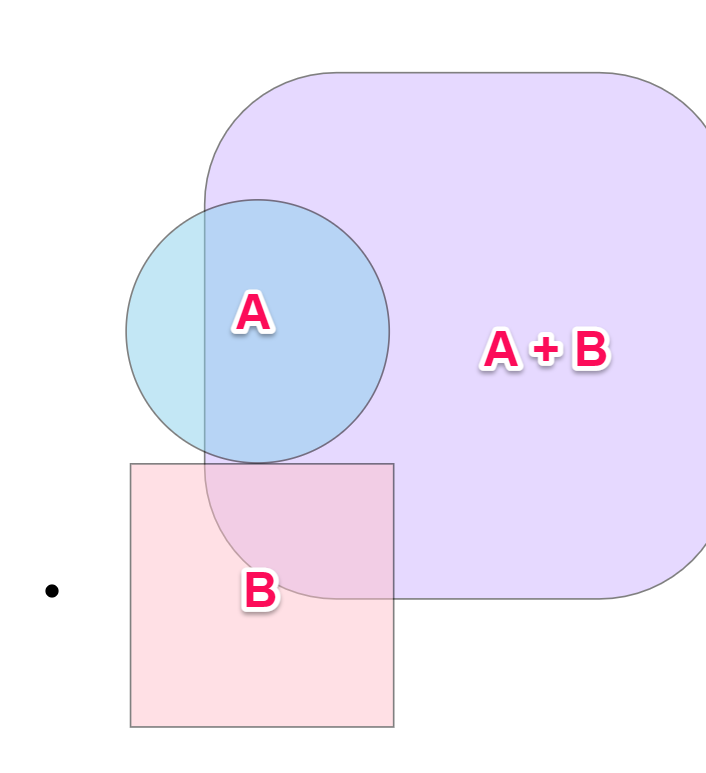
* Minkowski Sum
=> 두 다각형을 그리는 정점들의 합한 벡터들의 모양을 그린다.
( 원점 기준 표현 )
* Minkowski Difference
=> 두 다각형을 그리는 정점들의 차인 벡터들의 모양을 그린다.
( 원점 기준 표현 )

=> 원점이 포함되어진다면 두 물체는 overlap 되어진 상황.
즉,
정점들의 벡터 차를 원점 기준으로 그렸을 때, 도형이 원점을 포함한다면 겹쳐져있다는 개념을
활용해 두 물체의 겹쳐짐 여부를 판별 가능.
하지만,
원점 기준으로 물체를 그리는 연산을 컴퓨터에서 그대로 구현하기에는 계산량이 너무 많다.
어떻게 효율적으로 구현해야할까 ??
* Simplex
k-Simplex : shape that is guaranteed to enclose a point in k-dimensional space.
=> This is not entirely accurate, more precise and rigorous
definitions exist, but good enough for our use case.
원점을 포함할 도형.
즉,
원점을 포함하는 도형을 그리기 위해서 모든 벡터의 차를 구하기 보다는
원점을 포함하기 위한 도형을 우리가 정의한다.
이제부터 그것을 simplex 라고 부른다.
영문으로 나와있는 해석에서,
정확하지 않는 계산이지만 충분하다고 나오는데 위에 설명한 내용과 같다.
모든 벡터의 차를 구해 전체 도형을 그려서 확인하는 것이 아니라
우리는 전체 도형의 일부분인 simplex 도형을 그려서 확인하면 된다.
따라서,
원점을 포함하는 도형이기 위해선
2D 에선 '점 3개로 만든 삼각형' 이어야 하고
3D 에선 '점 4개로 만든 사면체' 이어야 한다.
이를 통해, 해당 도형이 원점을 포함하고 있는지 확인한다.

바로 구현을 들어가 이해하는 것보단
대략적인 과정을 어느 정도 숙지하고
구현 과정으로 들어가는 것이 이해하기 훨씬 쉬워보인다.
* GJK 알고리즘 적용 과정
모든 과정에서
A, B 도형이 존재, 임의의 기준이 되는 방향을 'D' 라고 가정한다.
@Support Function

임의의 방향 D 기준으로 A 도형 정점들 중 가장 먼 곳을 구한다. ( P1 )
B 도형에는 D 의 반대 방향 기준으로 가장 정점을 구한다. ( P2 )
두 정점을 뺀다. ( P1 - P2 )
이 과정을 'Support Function' 이라 부르겠다.
주의해야할 것은 도형을 그리는 선분 위의 정점이 아니라
도형을 이루는 정점을 대상으로 구한다는 것이다.
또한, Support Function 의 궁극적 의미는
'민코스키 차로 구해지는 도형의 D 방향으로의 최대 거리' 이다.
* 동작 과정
@1. 임의의 벡터 'D' ( 1,0,0 ) 으로 설정 후 Support Function 과정 수행.
이 값을 'X 벡터' 라 하고
X 벡터를 원점에서 표시한 점을 'X 정점' 이라 하겠다.
@2. 이번엔, X 벡터의 반대 방향 벡터 'D' ( -1, 0, 0 ) 로 둔다.
Support Function 과정을 이용해 다시 벡터를 구한다.
마찬가지로 Y 벡터, Y 정점이라 하겠다.
여기서 다시 되짚어보자면,
D 방향에 대해 Support Function 해 나온 벡터의 의미는
민코스키 차를 이용해 나온 도형에서 D 방향의 최대 벡터 크기라는 의미이다.
만약,
D ( 1,0,0 ) -> Support Function -> X
D (-1,0,0 ) -> Support Function -> Y 일 때
X 정점, Y 정점의 경우의 수는 총 3가지 영역이다.

* '2번 영역'에 해당하는지 확인하기 위해 어떻게 해야할까 ??
#1. SupportFunction 으로 구한 새로운 2번째 정점인 OY 가
Support Function 을 구할 때 사용한 D 와 같은 방향에 있지 않다면 불통.
위 그림에서 3번 영역이 걸러진다.
#2. ( X - Y ) 벡터와 OX 가 같은 방향에 있지 않다면 거른다.
위 그림에서 1번 영역이 걸러진다.
=> 위 과정을 거친 나머지가 2번의 영역에 해당한다.
이 때, #1 번에 해당하는 과정은 새로운 정점을 만들 때마다 확인해주어야 한다.
해당 과정을 'Sanity Check' 라고 하겠다.
따라서,
2번 상황 Y 정점에 대해서 Sanity Check 과정 을 수행.
@3. XY 벡터의 노멀벡터를 'D' 로 설정하고 SupportFunction 과정 수행.
마찬가지로 Z 벡터, Z 정점이라 하겠다.
해당 정점에 대해 Sanity Check 과정 수행.
X,Y,Z 세 정점으로 삼각형을 그릴 수 있는데,
이 때, 원점이 어떤 영역에 존재할 수 있는지는 총 '4가지' 이다.

S1 : ZY.cross(ZO).cross(ZY) (dot) ZO > 0 && ZX.dot ( ZO ) 인 영역
S3 : ZX.cross(ZO).cross(ZX) (dot) ZO > 0 && ZY.dot ( ZO ) 인 영역
S2 : S1, S3 빼고 나머지, 원점이 해당 삼각형 위에 있는 경우
S2 : 원점이 해당 삼각형 위에 없는 경우 ( 3차원 공간 )
=> 원점이 삼각형 위에 존재하거나 위 아래 쪽 3차원 공간에 존재한다면,
방향에 따라 XYZ 의 노멀벡터로 설정한 후, 다음 단계로 넘어간다.
@4. Support Function 과정 수행, W 정점을 구한다.
W 정점 Sanity Check 과정 수행
@5. XYZW 로 사면체를 만들고 각각의 삼각형의 노멀벡터를 구한다.
이 때, 원점과 같은 방향인지 확인한 후,
같은 방향이라면 해당 삼각형을 기준으로 이전 단계로 넘어간다.
모든 삼각형에 반대 방향을 만족한다면,
원점은 사면체 안에 있다는 뜻이므로 두 도형은 겹쳐져있다는 것이 증명된다.
* 정리
1. 임의의 방향 'D' 를 정한다.
2. Support Function ( 민코스키 차 ) 수행. -> ( X 정점 )
3. 반대방향을 'D' 로 설정 후, Support Function 수행. -> ( Y 정점 )
4. Y 정점에 대해 sanity check ( simplex 도형이 원점을 포함하는지 확인. )
5. XY 벡터의 normal vector 를 'D' 설정 후, Support Function 수행. -> ( Z 정점 )
6. Z 정점에 대해 sanity check
7. 그려진 simplex 도형이 원점을 포함하는지 확인.
8. 실패하면 이전 단계로 돌아감.
=> Sanity check 과정에 실패된다면 아예 겹쳐질 수 없음.
* 구현 ( 의사코드 )
* FindFurtherPoint
=> 방향을 기준으로 해당 Collider 정점과의 내적이 제일 큰 정점을 구함.
임의의 방향과 내적하면 임의의 방향에 대한 비율 ( 투영 ) 값이 나오기 때문
vec3 FindFurtherPoint(Collider A, vec3 Dir)
{
float maxValue = FLT_MIN;
for(vertex : A.verticeslist) -> 모든 정점
maxValue = max ( maxValue, Dir.dot(vertex) )
return maxValue;
}
* Support Function
=> FindFurtherPoint 를 이용해 SupportFunction 을 구현한다.
vec3 SupportFunction(Collider A, Collider B, vec3 Dir)
{
return FindFurtherPoint(A, Dir) - FindFurtherPoint(B, -Dir);
}
* Simplex
=> 원점을 포함할 도형 ( simplex ) 를 class 선언한다.
class Simplex
{
vec3 points[4] = { };
uint8 size = 0;
//클래스 초기화
//= { } 중괄호 대입연산자
Simplex& operator=( std::initializer_list<vec3> list)
push ( vec3 point )
vec3& operator[](const int idx){ return point[idx]; }
size();
}
* GJK Function
=> Simplex 도형의 정점들을 추가하며 Simplex 를 만들고 원점이 포함되는지 확인한다.
실패 시, 도형들의 정점을 제어하면서 과정을 반복한다.
bool GJK(Collider A, Collider B, vec3 Dir)
{
vec3 S = SupportFunction( A, B, vec(1,0,0) )
Simplex M;
M.push(S);
vec3 D = -S;
while(true)
{
vec3 A = SupportFunction ( A, B, D );
if( A.Dot(D) < 0 )
return false;
M.push(A);
if(DoSimplex(M, D))
return true;
}
}
* DoSimplex
=> Simplex 크기에 따라 각기 다른 정점 제어 방법을 실행.
bool DoSimplex(Simplex& M, vec3& D)
{
switch(M.size())
case 2 : return Line(M, D);
case 3 : return Triangle(M, D);
case 4 : return Tetrahedron(M, D);
return false;
}
* Line
=> Simplex 정점이 2개일 때, 3번째 정점을 그릴 수 있는지 확인.
원점이 D 내적 반경에 존재하면 해당 정점 2개의 직선의 외적을 구함.
아니라면, 원점을 포함하기 위해 D 를 원점 방향으로 바꿈.
=> 새로 추가된 정점을 a 로 둠.
bool Line(Simplex& M, vec3& D)
{
vec3 a = M[1];
vec3 b = M[0];
vec3 bo = -b;
vec3 ba = a - b;
if(ba.Dot(bo) > 0)
{
D = ba.cross(bo).cross(ba);
}
else
{
M = { b, };
D = bo;
}
return false;
}
* Triangle ( 삼각형 )
=> 여기서 중요한 것은,
Line 단계에서 통과된 경우가 Triangle 과정에 올라온 것이기 때문에,
A, B 정점을 잇는 벡터 사이에 원점이 있다.
bool Triangle(Simplex& M, vec3& D)
{
vec3 a = M[2];
vec3 b = M[1];
vec3 c = M[0];
vec3 ab = b - a;
vec3 ac = c - a;
vec3 ao = -a;
vec3 abc = ac.cross(ab);
if( ac.cross(abc) (dot) ao )
{
if( ac (dot) ao )
{
M = { c, a };
D = ac.cross(ao).cross(ac);
}
else
{
M = { b, a };
D = ab.cross(ab).cross(ab);
}
}
else
{
if( abc.cross(ab) (dot) ao )
{
M = { b, a };
D = ab.cross(ab).cross(ab);
}
else
{
if( abc.dot(ao) )
{
D = abc;
}
else
{
D = -abc;
M = { b, c, a };
}
}
}
}
* Tetrahedron ( 사면체 )
=> Simplex 도형 ( 사면체 ) 안에 원점이 존재하는지 판별.
=> 각 면의 normal 을 구하고 원점과 내적함으로써, 방향 확인.
=> 해당 삼각면 노멀벡터와 같은 방향으로 원점이 밖에 존재한다면,
해당 삼각면을 기준으로 Triangle 재실행.
bool Tetrahedron(Simplex& M, vec3& D)
{
vec3 a = M[3];
vec3 b = M[2];
vec3 c = M[1];
vec3 d = M[0];
vec3 ab = b - a;
vec3 ac = c - a;
vec3 ad = d - a;
vec3 ao = -a;
vec3 abd = ab.cross(ad);
vec3 abc = ac.cross(ab);
vec3 acd = ad.cross(ac);
if( abd.dot(ao))
{
return Triangle( { b, d, a }, abd );
}
else if( abc.dot(ao) )
{
return Triangle( { c, b, a }, abc );
}
else if( acd.dot(ao) )
{
return Triangle( { d, b, a }, acd );
}
return true;
}
* 결론
GJK 알고리즘의 핵심 개념은 Minkowski Difference 이다.
두 도형 A, B 가 있다고 가정할 때,
Minkowski Difference 를 이용해 나온 벡터들의 범위를 나타내면 도형이 나오는데
이 도형이 원점을 포함하고 있다면 A, B 는 겹쳐져있다고 증명될 수 있다.
해당 도형을 'Simplex' 라고 한다.
GJK 알고리즘이 효율적으로 활용되기 위해서,
도형들의 정점들을 이용해 나올 수 있는 Simplex 그려나가며
Simplex 가 원점을 포함하는지 계속 확인해 나가는 과정을 구현한다.
Support Function : 민코스키 차로 만든 도형에 방향 'D' 기준으로 최대 벡터를 구해준다.
Sanity Check : SupportFunction 으로 구한 벡터가 'D' 와 같은 방향인지 확인.
DoSimplex : 각 정점의 개수에 맞는 Simplex 도형을 그리며
원점이 포함되어지는지 확인해나간다.
최종적으로 모든 과정을 통과하면 A, B 도형은 overlap 되어졌다는 것을 알 수 있다.
주의해야할 것은
외적을 이용해야 하기 때문에 3차원을 기준으로 구현한다.
때문에 2D, 3D 에서의 다각형 충돌 모두 검사 가능하다.
참고 자료
https://www.youtube.com/watch?v=ajv46BSqcK4 ( gjk 알고리즘 )
'DirectX > 개념' 카테고리의 다른 글
| [DX]##3. 원근 투영 ( Perspective Projection ) (0) | 2022.12.16 |
|---|---|
| [DX] ##8. FRUSTUM CULLING ( 절두체 선별 ) (0) | 2022.08.25 |
| [DX] ##6. AABB, OBB 충돌 SAT 분리축 이론( Separating Axis Theorem ) (0) | 2022.08.05 |
| [DX] ##5. 직교투영, Screen Space ( Window Space ) (0) | 2022.08.02 |
| [DX] ##4. Z-Fighting (0) | 2022.07.31 |