* 정렬 알고리즘 ( Sort Algorithm )
정렬 알고리즘은 굉장히 다양하고
상황 마다 효율적인 알고리즘이 다를 수 있다.
우선 간단한 것부터 개념 정리를 할 것이고
정렬에 관한 내용을 갱신해가며 업데이트 할 예정이다.
( 아래에 구현된 코드는 검증되지 않은 코드이다. )
알고리즘을 만족하지 못하는 케이스가 있을 수 있다.
*선택 정렬 ( Selection Sort ) / O( N2 )
=> 처음부터 끝까지 탐색 후 데이터를 첫 순서 놓기 -> 2번째 idx 부터 끝까지 찾고 옮기기...
{ 1, 5, 10, 7, 2 }
{ 1, 5, 10, 7, 2 }
{ 1, 2, 10, 7, 5 }
{ 1, 2, 5, 7, 10 }
{ 1, 2, 5, 7, 10 }
void SelectSort(std::vector<int>& vec)
{
int size = vec.size();
for (int j = 0; j < size; ++j)
{
int Min = INT_MAX, idx = 0;
for (int i = j; i < size; ++i)
{
if (Min > vec[i])
{
Min = vec[i];
idx = i;
}
}
Swap(vec[j], vec[idx]);
}
}
*버블 정렬 ( Bubble Sort ) / O( N2 )
=> 앞 뒤 비교 -> j (맨 뒤) 는 확정적으로 순서가 정해짐. -> j - 1 까지 앞 뒤 비교....
{ 8, 3, 5, 4, 1 }
{ 3, 5, 6, 1, 8 }
{ 3, 5, 1, 6, 8 }
{ 3, 1, 5, 6, 8 }
{ 1, 3, 5, 6, 8 }
void BubbleSort(std::vector<int>& vec)
{
int size = vec.size();
for (int j = 0; j < size; ++j)
{
for (int i = 0; i < size - j - 1; ++i)
{
if (vec[i] > vec[i + 1])
{
Swap(vec[i], vec[i + 1]);
}
}
}
}
*삽입 정렬 ( Insertion Sort ) / O( N2 )
=> 계속 범위를 늘려간다. -> 범위만큼 계속 데이터를 삽입해가며 정렬해간다.
{ 1, 5, 3, 4, 2 }
{ 1, 5 } { 3, 4, 2 }
{ 1, 3, 5 } { 4, 2 }
{ 1, 3, 4, 5 } { 2 }
{ 1, 2, 3, 4, 5 }
=> 작은 정렬 기준으로
계속 옆으로 추가해주는 방식으로 행한다.
{ 1, 5 } <- 3 투입.
{ 1, 3, 5 } <- 4 투입.
void InsertSort(std::vector<int>& vec)
{
int size = vec.size();
for (int j = 1; j < size; ++j)
{
int InsertValue = vec[j], Pos = 0;
for (int i = j; i > 0; --i)
{
if (InsertValue < vec[i - 1])
{
vec[i] = vec[i - 1];
continue;
}
else
{
Pos = i;
break;
}
}
vec[Pos] = InsertValue;
}
}
*힙 정렬 ( Heap Sort ) / O( NlogN )
=> 힙 트리로 구현된 '우선순위 큐' 활용.
* 힙트리
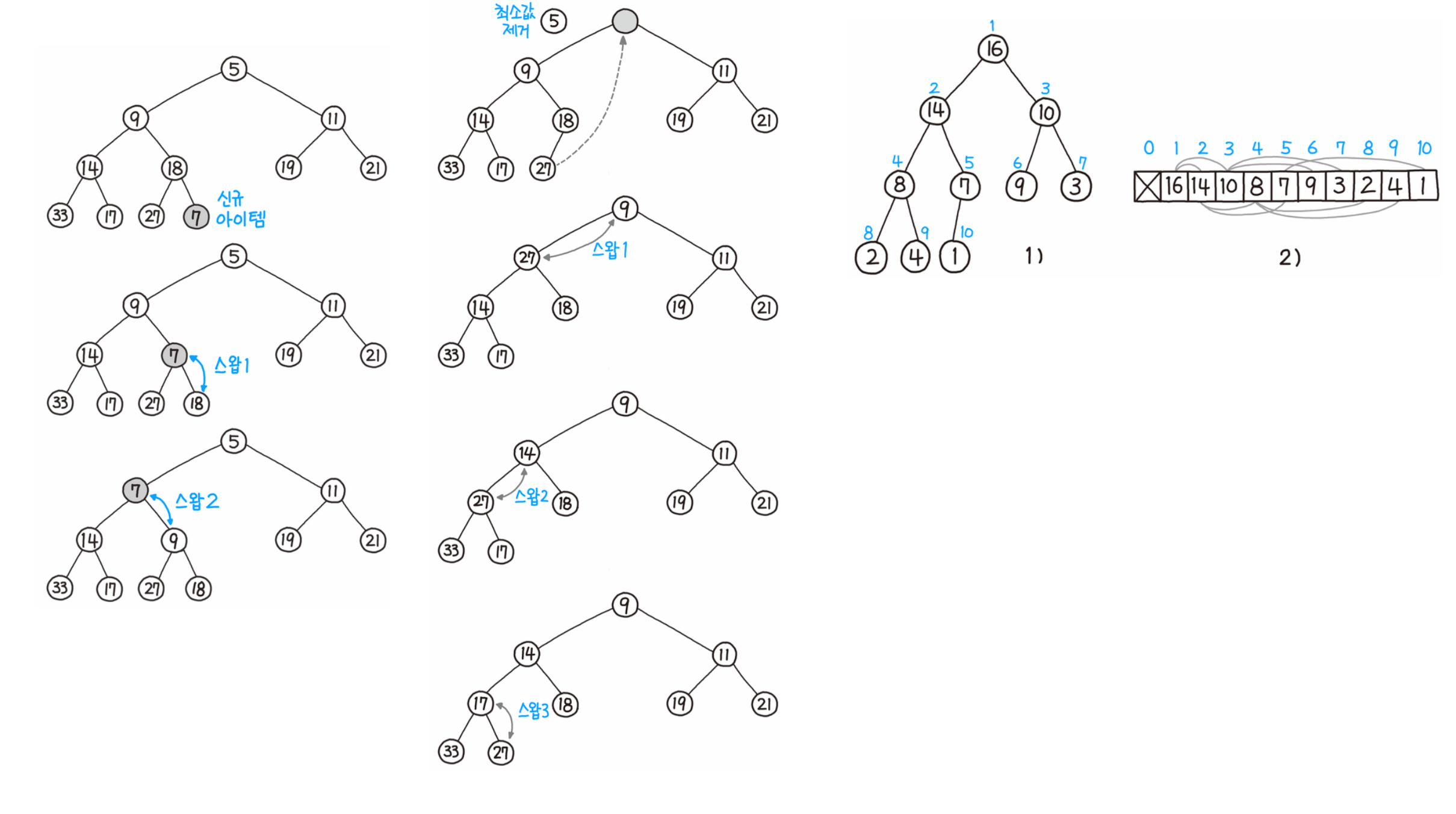
void HeapSort(std::vector<int>& vec)
{
std::priority_queue<int> pq;
int size = vec.size();
for (int i = 0; i < size; ++i)
{
int in = (-1) * (vec[i]);
pq.push(in);
}
int idx = 0;
while (!pq.empty())
{
int out = (-1) * pq.top();
pq.pop();
vec[idx] = out;
++idx;
}
}
*병합 정렬 ( Merge Sort ) / O( NlogN )

=> 대표적인 분할 정복 예시
분할 ( Divide ) : 문제를 더 단순하게 분할.
정복 ( Conquer ) : 분할된 문제를 해결.
결합 ( Conbine ) : 결과를 취합해 마무리.
=> 이진 탐색과 유사한 개념.
재귀적으로 나누고 합친다.
=> 합치는 경우
{ 1, 9 } { 4, 5 } 일 때,
{ 1 }
{ 1, 4 }
{ 1, 4, 5 }
{ 1, 4, 5, 9 }
void MergeSort(std::vector<int>& vec,int Start, int End)
{
if (Start >= End) return;
int Mid = (Start + End) / 2;
MergeSort(vec, Start, Mid);
MergeSort(vec, Mid + 1, End);
Merge(vec, Start, Mid, End);
}
void Merge(std::vector<int>& vec, int Start, int Mid, int End)
{
std::vector<int> temp;
int P1 = Start, P2 = Mid + 1;
while (P1 <= Mid && P2 <= End)
{
if (vec[P1] <= vec[P2])
{
temp.push_back(vec[P1]);
P1++;
}
else if (vec[P1] > vec[P2])
{
temp.push_back(vec[P2]);
P2++;
}
}
while (P1 <= Mid)
{
temp.push_back(vec[P1]);
P1++;
}
while (P2 <= End)
{
temp.push_back(vec[P2]);
P2++;
}
for (int i = 0; i < temp.size(); ++i)
{
vec[i + Start] = temp[i];
}
}
* 퀵 소트 ( Quick Sort )
조건 최악일 때, O( N2 )
* 최악의 상황은 언제인가 ??
=> 한번의 과정에서,
pivot 값이 최댓값, 최솟값일 때 그 과정은 최악이다.
또한,
pivot 값이 최댓값, 최솟값이 연속적인 상황은
오름차순, 내림차순 으로 정렬되어있을 때이다.
*그렇다면 최악의 상황이 O( N2 ) 인 퀵소트는 왜 빠르다고 하는것일까 ??
1. 어떤 임의로 추가된 데이터들이 정렬되어있을 확률은 거의 없다.
( 물론, 이전에 정렬을 적용하지 않은 상황. )
만약,
1,2,3,4,5,6,7,8,9 범위의 데이터가 임의로 추가될 때,
오름차순 or 내림차순으로 될 확률은 거의 없다. ( 1 / 210 )
2. 불필요한 데이터 복사가 필요없다.
앞서 본 힙, 병합 정렬 같은 경우
어떤 컨테이너를 거쳐서 그 컨테이너를 복사하는 과정이 필요한데,
퀵소트는 이런 부가적인 연산이 필요없다.
3. 메모리가 연속적이므로 캐쉬 Hit 율이 높다. ( 빠르다. )
=> 결론적으로,
퀵소트의 최악의 상황을 면하기 위해,
pivot 선정 시 최대, 최소인 값을 선택하지 않는 알고리즘을 적용한다면
'어떤 상황에서든 평균적인 속도' 가 나올 것이다.
*동작과정

void QuickSort(std::vector<int>& vec, int Start, int End)
{
if (Start >= End) return;
int Mid = (Start + End) / 2;
int Pivot = Start, low = 1, high = End;
while (low < high)
{
while (vec[Pivot] >= vec[low] && low < End)
{
low++;
}
while (vec[Pivot] < vec[high] && high > Start)
{
--high;
}
if(low < high)
Swap(vec[low], vec[high]);
}
Swap(vec[high], vec[Pivot]);
Pivot = high;
QuickSort(vec, Start, Pivot - 1);
QuickSort(vec, Pivot + 1, End);
}
참고 링크
'알고리즘 > 개념' 카테고리의 다른 글
| [Algo]@Disjoint Set ( 상호 배타적 집합 ) (0) | 2022.08.09 |
|---|